Прямая и плоскость. Краткий обзор определений, формул.

Уравнение прямой на плоскости, проходящей через данную точку перпендикулярно данному вектору, в векторной и координатной форме

В прямоугольных декартовых системах координат нормальное уравнение прямой записывается как $(\vec{r},\vec{n})=D$ или $A(x-x_0)+B(y-y_0)=0$. Соответственно данный вектор -- вектор нормали $\vec{n}$.

Уравнение прямой на плоскости, проходящей через данную точку параллельно данному вектору, в векторной и координатной форме

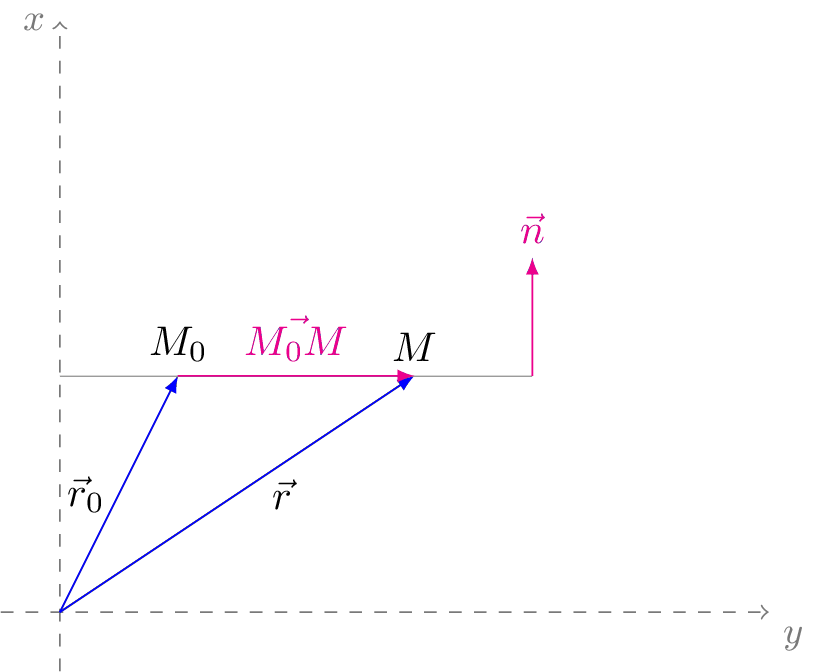
Векторно: $\vec{r}=\vec{r}_0+\alpha\vec{a},$ где $\vec{a}$ -- направляющий вектор прямой.

Легко перейти к координатному виду. Пусть $\vec{r}(x,y)$, $\vec{r_0}(x_0,y_0)$, $\vec{a}(a_1,a_2)$.

Тогда

$$ \begin{cases} x-x_0=\alpha a_1 \cr y-y_0=\alpha a_2 \end{cases} $$

Избавившись от параметра, получим каноническое уравнение прямой на плоскости:

$$ \frac{x-x_0}{a_1}=\frac{y-y_0}{a_2} $$

Перемножив крест-накрест, можем переписать в виде

$$ \begin{gathered} a_2x-a_1y+(a_1y_0-a_2x_0) \cr Ax+By+C=0 \end{gathered} $$

где $A=a_2$, $B=-a_1$, $C=a_1y_0-a_2x_0$.

Данный вектор $\vec{a} (-B, A)$

Уравнение прямой на плоскости, проходящей через две данные точки

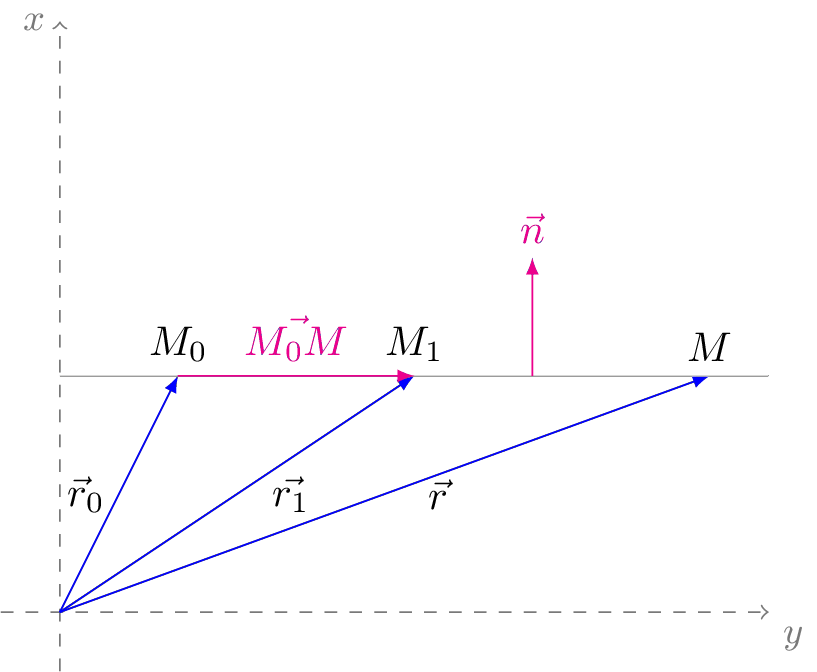
Легко вывести из предыдущего, взяв в качестве направляющего вектора вектор между двумя известными точками примой.

$$ \frac{x-x_0}{x_1-x_0}=\frac{y-y_0}{y_1-y_0} $$

Параметрические уравнения прямой на плоскости, проходящей через данную точку параллельно данному вектору, в векторной и координатной форме

Векторно: $\vec{r}=\vec{r}_0+\alpha\vec{a}$, где $\vec{a}$ -- направляющий вектор прямой.

Координатно:

$$ \begin{cases} x-x_0=\alpha a_1 \cr y-y_0=\alpha a_2 \end{cases} $$

Нормальное уравнение прямой на плоскости

Уравнение вида $$\cos\alpha\cdot x + \cos\beta\cdot y = p $$ называется нормальным уравнением прямой.

• $\alpha$ -- угол между $\vec{n}$ и положительным направлением оси $x$,
• $\beta$ -- угол между $\vec{n}$ и положительным направлением оси $y$,
• $p$ -- расстояние от начала координат до прямой.

Параметрические уравнения прямой в пространстве

Аналогично прямой в плоскости прямую можно описать уравнением

$$ \vec{r}=\vec{r}_0+\alpha\vec{a} $$

и записать его в параметрическом виде:

$$ \begin{cases} x=x_0+\alpha a_1 \cr y=y_0+\alpha a_2 \cr z=z_0+\alpha a_3 \end{cases} $$

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору, в векторной и координатной форме

$$ A(x-x_0)+B(y-y_0)+C(z-z_0)=0 $$

где данный вектор - вектор нормали $\vec{n}(A,B,C)$, данная точка $M$ -- $(x_0,y_0,z_0)$

Иначе говоря,

$$ (\vec{r}-\vec{r}_0,\vec{n})=0 \Longrightarrow (\vec{r},\vec{n})=D $$

Уравнение плоскости, проходящей через данную точку параллельно двум данным векторам, в векторной и координатной форме

Вектора $\vec{M_0M}=\vec{r}-\vec{r}_0$, $\vec{a}$ и $\vec{b}$ должны быть компланарны, т.е. их смешанное произведение равно нулю:

$$ (\vec{r}-\vec{r}_0,\vec{a},\vec{b})=0 $$

или координатно

$$\begin{vmatrix}x-x_0 & y-y_0 & z-z_0\cr a_1 & a_2 & a_3 \cr b_1 & b_2 & b_3\end{vmatrix}=0$$

Уравнение плоскости, проходящей через три данные точки

Пусть точки $A(a_1,a_2,a_3)$, $B(b_1,b_2,b_3)$, $C(c_1,c_2,c_3)$. Тогда можно свести к предыдущему случаю, взяв два вектора $\vec{AB}$ и $\vec{AC}$, и точку $A$:

$$ \begin{vmatrix} x-a_1 & y-a_2 & z-a_3 \cr b_1-a_1 & b_2-a_2 & b_3-a_3 \cr c_1-a_1 & c_2-a_2 & c_3-a_3 \cr \end{vmatrix}=0 $$

Параметрические уравнения плоскости, проходящей через данную точку параллельно двум данным векторам, в векторной и координатной форме

$$ \vec{r}=\vec{r}_0+\alpha_1\vec{a}+\alpha_2\vec{b} $$

и

$$ \begin{cases} x=x_0+\alpha_1 a_1 +\alpha_2 b_1 \cr y=y_0+\alpha_1 a_2 +\alpha_2 b_2 \cr z=z_0+\alpha_1 a_3 +\alpha_2 b_3 \end{cases} $$

Нормальное уравнение плоскости

Уравнение вида $$\cos\alpha\cdot x + \cos\beta\cdot y + \cos\gamma\cdot z = p $$ называется нормальным уравнением плоскости.

• $\alpha$ -- угол между $\vec{n}$ и положительным направлением оси $x$,
• $\beta$ -- угол между $\vec{n}$ и положительным направлением оси $y$,
• $\gamma$ -- угол между $\vec{n}$ и положительным направлением оси $z$,
• $p$ -- расстояние от начала координат до плоскости.

Каноническое уравнение прямой в пространстве

Записывается как

$$ \frac{x-x_0}{a_1}=\frac{y-y_0}{a_2}=\frac{z-z_0}{a_3} $$

где $\vec{a}(a_1,a_2,a_3)$ -- направляющий вектор этой прямой.