Pgfplots: краткое руководство – Блог Федора Сарафанова

О пакете

Пакет pgfplots представляет собой мощный инструмент, предназначенный для создания научных графиков. Он создан на базе tikz, не менее прекрасного пакета, который позволяет создавать векторную графику прямо на латехе.

Если вы сомневаетесь в необходимости использования pgfplots или tikz, посмотрите на простые графики, созданные с помощью этих пакетов:

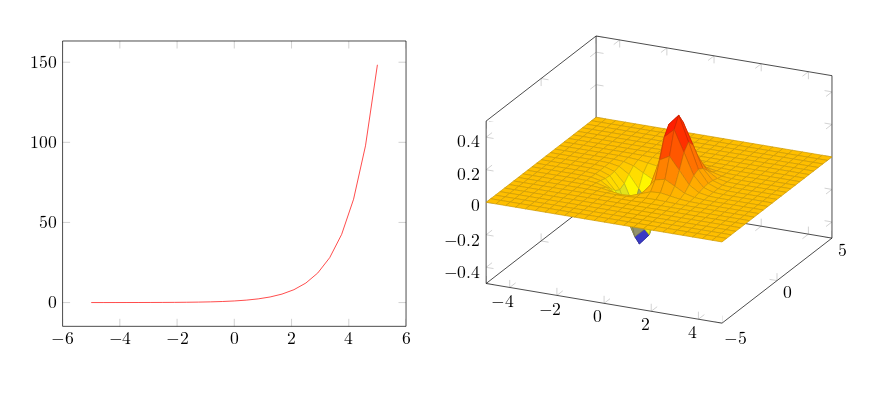
Много небольших примеров применения можно посмотреть в галерее pgfplots ¹.

Основная идея pgfplots - упрощение включения графиков в документ. Задача пользователя - задать формулу или данные, а остальным занимается pgfplots. Так, код графиков (см. пример на overleaf), приведенных выше (без преамбулы) выглядит так:

% Код первого графика
\begin{tikzpicture}
	\begin{axis}
		\addplot[color=red]{exp(x)};
	\end{axis}
\end{tikzpicture}

% Код второго графика
\begin{tikzpicture}
	\begin{axis}
		\addplot3[surf] {exp(-x^2-y^2)*x};
	\end{axis}
\end{tikzpicture}

Заметьте, от пользователя в простейшем случае не потребовалось практически ничего, кроме задания функции и вида её отображения. Разумеется, можно и вручную задать пределы построения функции и многое другое.

0. Введение в pgfplots
1. Математика в pgfplots
2. Объявление новых функций
- 2.1. Составление функции Хевисайда. Ступенька произвольной длины
3. Настройка осей и сетки
4. Легенда графика
5. Построение графика
6. Особенности построения графиков
The End. Рекомендуемые источники

0. Введение в pgfplots

0.1. Преамбула

Подключается пакет стандартным образом. Вставьте этот код в преамбулу (до \begin{document}):

\usepackage{pgfplots}

Так же можно сразу в преамбуле сделать некоторые настройки. Во-первых, можно задать используемую версию pgfplots. Так как пакет динамично развивается, то некоторые вещи становятся несовместимыми от версии к версии. Наиболее разумным является использование текущей версии указанием параметра

\pgfplotsset{width=10cm,compat=newest}

но после окончания работы неплохо бы указать текущую версию вручную, чтобы если вдруг у вас будет такая функциональность, что не будет работать в следующих версиях, это не помешало бы компилировать график спустя длительное время.

Параметр width задает ширину графика. Также можно задать и высоту height. Надо заметить, что это нововведение по сравнению с tikz: в tikz картинки изменяют свой размер соответственно содержимому, pgfplots же может подогнать содержимое (масштабом осей) под график. Надо заметить, что возможно и обратное - задавать вручную масштаб осей, тогда высота и ширина будут определяться ими и содержимым, а параметры width, height будут игнорироваться.

0.2. Окружение осей

Поскольку pgfplots основан на tikz, график должен находиться в окружении tikzpicture. Сам график строится в осях (полотно графика с системой координат и некоторым масштабом).

Оси задаются окружением \begin{axis} ... \end{axis}. У осей могут быть свои параметры:

\begin{tikzpicture}
	\begin{axis}[
			%axis,          % Обычные оси
			%semilogxaxis,	% По оси x логарифмический масштаб
			%semilogyaxis,  % По оси y логарифмический масштаб
			%loglogaxis,    % По обоим осям логарифмический масштаб
			enlargelimits=true, % Делать размер осей чуть больше графика
		]
		\addplot[color=red]{ln(x)};
	\end{axis}
\end{tikzpicture}

Булев параметр enlargelimits, если он включен, делает размер рисунка немного больше, так, чтобы нарисованные графики не касались края рисунка, а оставалось некоторое расстояние. По умолчанию он включен, и отключать его почти никогда не требуется.

Здесь они закомментированы. Достаточно одного из параметров, причем параметр axis используется по умолчанию, и его можно не указывать.

Чтобы добавить график, используется команда

\addplot[color=red]{ln(x)};

Внутри квадратных скобок могут быть переданы некоторые параметры, например здесь указан цвет линии графика. Квадратные скобки обязательны, если не передано ни одного параметра, нужно оставить между ними пробел.

Важно, что все команды (эта необходимость тянется из пакета tikz) должны заканчиваться точкой с запятой.

Внутри фигурных скобок размещается функция, задающая график. О её составлении рассказано ниже.

Так же более подробно о настройке осей и сетки см. раздел 3 "Настройка осей и сетки"

Самое подробное описание (на английском) можно найти в мануале по pgfplots ².

0.3. Пакет standalone: графики в отдельных файлах

Компиляция графиков pgfplots может быть долгой. Особенно это касается случаев, когда строится функция с большим числом точек, уходящая на бесконечность или обрабатываются большие экспериментальные данные из файла.

В таком случае разумно, чтобы сократить время компиляции, создавать каждый рисунок как отдельный pdf-документ, а затем подключать его как картинку. С одной стороны, увеличивается скорость компиляции, с другой, документ становится проще за счет выноса длинного кода в отдельные файлы, а структура документа становится более гибкой: отдельный график можно использовать в других проектах.

Настоятельно рекомендуется использовать именно этот способ. Для него достаточно указать классом документа standalone, и документ будет компилироваться в pdf файл, причем так, что поле документа будет обрезано до размеров графика.

Стоит отметить, что этот пакет конфликтует с пакетом geometry, и последний использовать в документах класса standalone не нужно.

Дочерний документ (например, это файл img/ris1.tex):

\documentclass{standalone}

\usepackage[utf8]{inputenc}
\usepackage{pgfplots}
\pgfplotsset{width=10cm,compat=1.9}

\begin{document}
	\begin{tikzpicture}
		\begin{axis}
			\addplot[color=red]{exp(x)};
		\end{axis}
	\end{tikzpicture}
\end{document}

Вставка картинки в основной документ:

\begin{figure}[h!]
	\centering
	\includegraphics[scale=1]{img/ris1}
	\caption{Наш отдельный график}
	\label{fig:ris1}
\end{figure}

1. Математика в pgfplots

Математический аппарат pgfplots-а принадлежит пакету более низкого уровня pgf. Математические возможности pgf достаточно велики, и мы рассмотрим только некоторые аспекты составления сложных функций для построения различных графиков.

1.1. Стандартные операторы

Без пояснения: +,-,*,/,^
Сравнение: >,>=,<=,==,!=
Оператор факториала: x! аналогичен вызову функции factorial(x)

Отдельно стоит сказать об условном операторе x ? y : z. Он вернет y, если x истина, и z, если ложь. Это можно использовать, например, для построения функций Хевисайда, о чем будет сказано ниже.

1.2. Стандартные функции

div(x,y) - целочисленное деление
mod(x,y) - остаток от деления
sign(x) - знак числа

Также ряд функций, не нуждающихся в объяснениях: factorial(x), sqrt(x), exp(x), ln(x), log10(x), log2(x), abs(x)

Функции округления

round(x) - округлит до ближайшего целого, большего по модулю чем округляемое, числа: 1.5->2, -1.5->-2
floor(x) - округлит х до ближайшего целого числа в большую сторону
ceil(x) - округлит х до ближайшего целого числа в меньшую сторону
int(x) - просто вернет целую часть x
frac(x) - вернет дробную часть x

Целочисленные функции

iseven(x), isodd(x) - проверяет четность (нечетность) числа, в случае успеха вернет 1, в случае неудачи 1
isprime(x) - проверяет, простое ли число (аналогично вернет 1/0)

Тригонометрические функции

sin,cos,tan,sec,cosec,cot,asin,acos,atan

Важно заметить, что все тригонометрические функции принимают на вход число в градусах, а для перевода из радиан в градусы служит функция deg, а обратно - rad. Это поведение по умолчанию, его можно поменять:

\pgfkeys{/pgf/trig format=rad|deg}

Кроме того, можно использовать радианы и не изменяя поведение по умолчанию - указать, что аргумент дан в радианах: cos(pi/2 r) ->0.

Гиперболические функции

sinh,cosh,tanh

1.3. Генерация случайных чисел

Присутствует и возможность генерации случайных чисел: вызов rnd вернет случайное число от 0 до 1, rand от -1 до 1.

Более подробно о функциях и операторах можно почитать в руководстве по pgf, 1000-1011 страницы ³.

2. Объявление новых функций

\begin{tikzpicture}[
	  declare function={
	    myfun(\x,\t) = (\x*\t);
	  }
  ]
	\begin{axis}
		\addplot[color=red, domain=0:4, samples=300]{myfun(x,2)};
	\end{axis}
\end{tikzpicture}

Объявляется новая функция для всего рисунка. Все должно быть понятно из примера.

2.1. Составление функции Хевисайда. Ступенька произвольной длины

Используя условный оператор, несложно составить функцию Хевисайда:

1*(x>0 ? 1 : 0)

Очевидно, она будет равна множителю перед скобкой при x>0 и нулю в отрицательной области. Из двух функций Хевисайда можно составить и прямоугольный импульс:

1*(x>0 ? 1 : 0)-1*(x>1 ? 1 : 0)

Это прямоугольный импульс, начинающийся от нуля. Однако, можно создать функцию с аргументами высоты, ширины и начала ступеньки:

Нажмите для просмотра результата

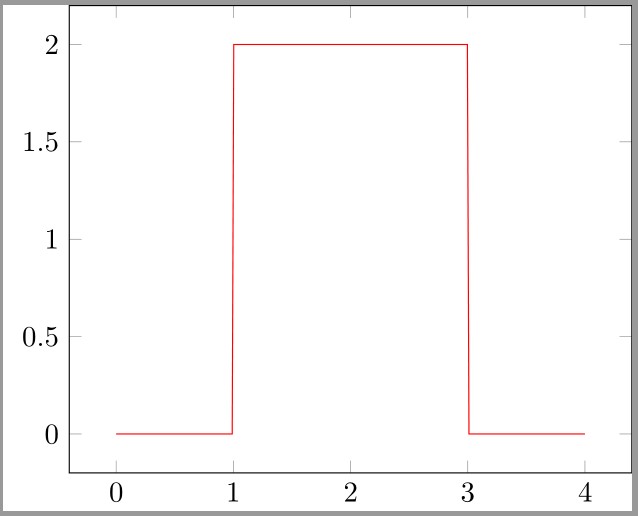
\begin{tikzpicture}[
	  declare function={
	    impuls(\h,\w,\b,\x) = \h*((\x>\b ? 1 : 0)-(\x>(\b+\w) ? 1 : 0));
	  }
  ]
	\begin{axis}
		\addplot[color=red, domain=0:4, samples=300]{impuls(2,2,1,x)};
	\end{axis}
\end{tikzpicture}

Заметим, что в общем случае, например для построения кусочно-гладких функций, необязательно создавать громоздкую функцию, которая будет включать в себя все остальные с помощью условного оператора.

Если заранее известно, что функция будет без скачков (скачок сам по себе можно построить, но особого смысла нет), то можно воспользоваться тем, что команда \addplot имеет параметр области построения графика domain=start:end и использовать несколько плотов:

\begin{tikzpicture}
	\begin{axis}
		\addplot[color=red, domain=0:1, samples=300]{x^2};
		\addplot[color=red, domain=1:4, samples=300]{2*x};
	\end{axis}
\end{tikzpicture}

samples здесь - количество точек графика. График не может строиться абсолютно непрерывно и берется в некотором числе точек, которые соединяются отрезками: чем выше число точек, тем качественнее картинка, но и медленнее её компиляция и отрисовка. Разумно делать это число меньше для медленно меняющихся графиков и много больше для быстро меняющихся, особенно для таких, как в предыдущем примере - со скачком.

По мере чтения руководства читатель может заметить появление новых параметров без объяснения. Предполагается, что они могут быть интуитивно понятны.

3. Настройка осей и сетки

3.1. Оси и их подписи. Заголовок графика.

Рассмотрим базовый пример настройки осей. По умолчанию, вместо координатных осей рисуется прямоугольник координат (axis lines = box), как это часто принято в научных статьях. Однако никто не мешает использовать оси-стрелки, или вообще отключить оси:

\begin{tikzpicture}
\begin{axis}[
    axis lines = middle, % привычные оси со стрелочками с пересечением в нуле
    % возможные значения: box, left, middle, center, right, none
    xlabel = {$x$}, % подпись оси x
    ylabel = {$f(x)$}, % подпись оси y
    title={Мой первый график $f(x)=x^2 - 2\cdot x - 1$}, 
]
	\addplot[domain=-10:10, samples=100, color=red] {x^2 - 2*x - 1};
\end{axis}
\end{tikzpicture}

Обратите внимание на то, что у нас появился параметр title, задающий заголовок графику. Как правило, при использовании пакета standalone, это не нужно - заголовок графика задается командой caption в окружении figure.

Вообще говоря, положение осей можно применять и по отдельности:

  axis x line=center,
  axis y line=left,

Можно задать и определенные правила отрисовки осей, например цвет, или сделать их пунктиром (dashed):

  x axis line style ={black!40, dashed},
  y axis line style ={red},

Заметьте, как здесь указывается цвет. Это обозначение black!40!red означает смешение цветов, в соотношении 40% black 60% red, если цвет справа не указан, то он берется белым: значит, black!40 даст нам серый цвет. Таким образом из базовых цветов можно составить любой цвет.

Также можно перенести подписи осей к стрелкам на осях:

  xlabel style={below right},
  ylabel style={above left, red, scale=1.5},

Здесь появился новый параметр scale, подпись к оси y будет в полтора раза больше, чем к оси x, очевидно.

Подразумевается, что все приведенные выше параметры подставляются в параметры окружения axis.

3.2. "Тики" (метки на осях) и их подписи

Когда график не качественный, важно наиболее удобно показать подписи (числа) к осям. За них отвечают ticks (тики) - маленькие перпендикулярные черты к осям с численной подписью.

Настройка расстояния между тиками:

xtick distance=1,
ytick distance=2

Также можно вручную указать список основных тиков:

xtick={0,20,40,60,80,100}, 
ytick={0,20,40,60,80,100,120}

А при необходимости, можно задать и подписи к ним (по умолчанию подпись - это координата тика):

ytick={1.5707,0.7853,1}, 
yticklabels={$\frac{\pi}{2},$, $\frac{\pi}{4}$, 1},

По умолчанию pgfplots пытается подобрать наиболее разумное расположение тиков.

3.2.1. Дополнительные тики

Иногда требуется специально показать положение чего-либо на осях. Для этого можно использовать дополнительные тики, задав им координаты и их подписи:

extra y ticks={-9/16,-6/16},	% положение дополнительных тиков
extra y tick labels={	% их подписи
 		{$U_{min}$}, {$U_{min}+\Delta U$}
},

Для x аналогично.

3.2.2. Промежуточные тики (minor ticks)

Часто кроме основных меток на осях, ставят промежуточные: так, например, на линейке отмечены сантиметры рисками с подписями, а миллиметры просто рисками без подписей.

Такое задается с помощью minor ticks:

 minor tick num = 2,

Этот параметр задает количество таких тиков (эквидистантных) между основными (major) тиками для обоих осей одинаково. А можно задать и для каждой оси отдельно:

 minor x tick num=3,
 minor y tick num=8,

3.3. Максимальные и минимальные значения на графике. Масштаб осей

Масштаб осей задан в виде <длина орта x> <длина орта y>:

  unit vector ratio = 1 1,
  xmax = 8,
  xmin=-2,
  ymax=1.5,
  ymin=-0.2,

Максимальные и минимальные значения заданы очевидным образом.

3.4. Сетка. Единицы измерения в LaTeX

3.4.1. Сетка через основные и промежуточные тики

Сетка всегда проходит через тики на осях. Она может проходить как через основные (major) так и через промежуточные (minor) тики:

  grid=major, % м.б. еще both - и там и там
  grid style={dotted, cyan},

Причем стиль можно задать как всей сетке (и основной major и промежуточной minor), так и по отдельности:

  minor grid style={dashed,red, line width=0.2pt},
  major grid style={solid,black, line width=0.1pt},

Обратите внимание на используемые единицы измерения. em - это высота одной буквы шрифта 10pt:

pt называется типографским пунктом.

3.4.2. Сетка через дополнительные (extra) тики

По умолчанию, сетка автоматически проведет линии и через пользовательские (дополнительные) тики, но этот стиль можно модифицировать:

  extra tick style={grid=major, grid style={dotted, cyan}},

Здесь мы скопировали стиль основных линий сетки и модифицировали его, сделав в точечку (dotted) и голубым (cyan).

4. Легенда графика

Для того, чтобы сопоставить какому-либо графику, который строится с помощью \addplot, элемент легенды, есть специальная команда \addlegendentry, которую нужно разместить после \addplot:

\begin{tikzpicture}
\begin{axis}[
    axis lines = middle,
    xlabel = {$x$},
    ylabel = {$f(x)$},
    title={Мой первый график $f(x)=x^2 - 2\cdot x - 1$}, 
    legend pos={south west},
]
	\addplot[domain=-10:10, samples=100, color=red] {x^2+2*x};
	\addlegendentry{$x^+2\cdot x$};
\end{axis}
\end{tikzpicture}

Здесь появился параметр legend pos, который задает положение легенды на графике:

legend pos=south west|south east|north west|north east

5. Построение графика

В самом начале мы рассмотрели и далее неоднократно употребляли построение графика заданной функции \(y=f(x)\). Однако, часто требуется построить не такой (или не только такой график), а покоординатный график (или, как это говорят математики, функция задана таблично, а не аналитически).

Обычно такая задача возникает при обработке экспериментальных данных. Есть два способа: записать данные непосредественно в график, или записать их в текстовую таблицу (tsv или csv). Рассмотрим такие случаи.

5.1. Чтение данных из таблицы

Важно: для чтения из таблицы нужно подключить пакет:

\usepackage{pgfplotstable}

Рассмотрим такой пример: пусть у нас есть файл data.tsv, лежащий в той же папке, что и рисунок:

Fr	Uin err
15	7.446	0.1
25	7.532	0.1
40	7.512	0.1
100	7.412	0.1
200	7.41	0.1
300	7.32	0.1
400	7.27	0.1
500	7.236	0.1
1000	7.3	0.1
2000	7.282	0.1
3000	7.27	0.1

Тогда его можно построить командой:

\addplot +[blue, dashed] 
	plot table [		    	    	    	
		x=Fr, 
		y=Uin
	]{data.tsv};

В этом примере все просто. В первых квадратных скобках пишутся параметры, управляющие отрисованным графиком, построением прямоугольников ошибок и т.п., а во вторых - параметры чтения из таблицы, создание новых столбцов таблицы путем математического выражения, составленного из существующих столбцов, о чем написано ниже.

5.1.2. Создание новых стоблцов таблицы

Рассмотрим простой пример, на основе приведенного выше файла данных. В нем в первой столбце стоит частота в герцах, но допустим, что мы хотим построить график от круговой частоты, т.е. домножить на \(2\pi\):

\addplot +[blue, dashed] 
	plot table [		    	    	    	
		create on use/omega/.style={
		    create col/expr={
		    \thisrow{Fr}*2*pi
		    }
		},	
		x=omega, 
		y=Uin
	]{data.tsv};

Здесь видно, как несложно оперировать созданием новых столбцов. При этом применима вся математика, рассмотренная в разделе выше.

5.2. Маркеры на линии графика

Часто требуется не просто соединить экспериментальные точки линией, а указать каждую конкретную точку маркером (mark), а то и вовсе составить график только из маркеров. Для этого предыдущий пример несложно модифицируется:

\addplot +[blue, mark=*, mark size=1.5pt, only marks] 
	plot table [		    	    	    	
		create on use/omega/.style={
		    create col/expr={
		    \thisrow{Fr}*2*pi
		    }
		},	
		x=omega, 
		y=Uin
	]{data.tsv};

Параметр only marks принуждает рисовать только маркеры, без линии их соединяющих, mark size размер маркера, mark тип маркера.

Существует достаточно много типов:

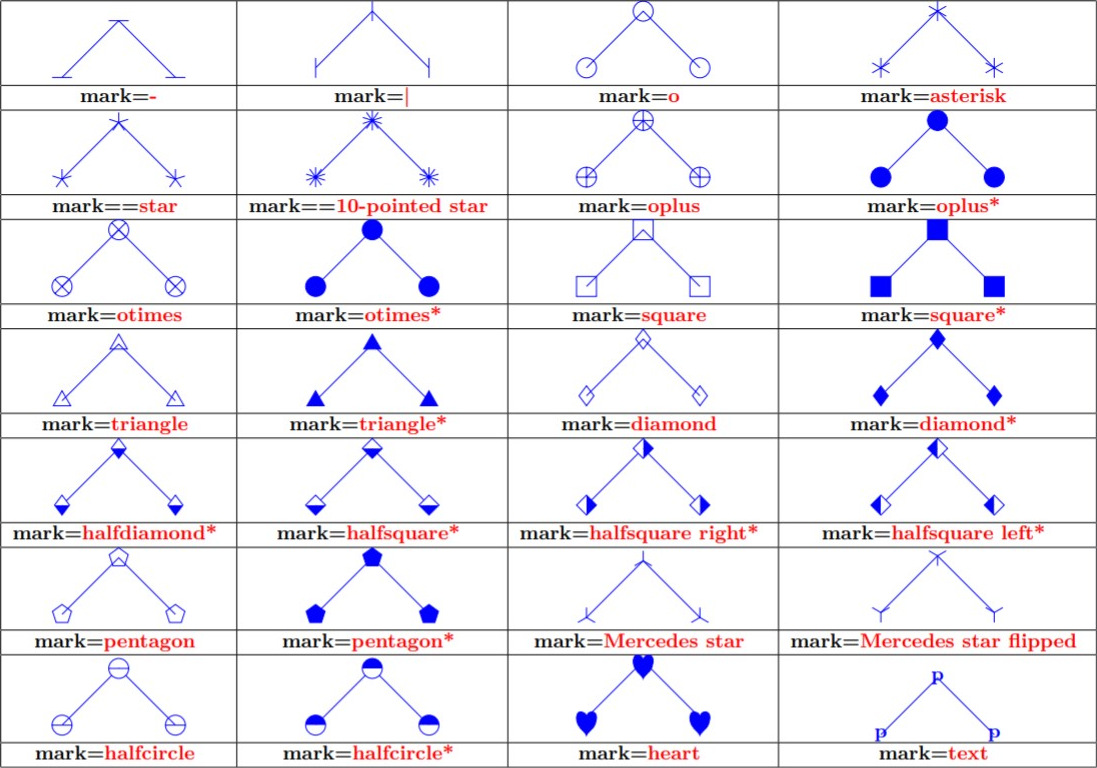
Эта картинка взята из руководства по tikz в картинках ⁴.

Для маркеров можно сразу задать несколько параметров: вместо размера задать масштаб (второй способ изменить размер маркера, иногда более удобный), основной цвет (draw) и цвет заливки (fill

\addplot +[
	mark=*, 
	mark options={
		scale=2,
		fill=blue,
		draw=red,
	},
	only marks
] plot table [		    	    	    	
		create on use/omega/.style={
		    create col/expr={
		    \thisrow{Fr}*2*pi
		    }
		},	
		x=omega, 
		y=Uin
	]{data.tsv};

5.3. Прямоугольники ошибок

Для начала рассмотрим простейший случай постоянной ошибки. Параметры прямоугольников ошибок пишутся в параметры команды plot. Рассматривать будем все на примере ошибки по y, по другим осям анологично с точностью до замены y->x,z.

Для включения прямоугольников ошибки и возможности их настройки перед последующими рассмотренными параметрами нужно вставлять параметр error bars/.cd.

5.3.1. Постоянная абсолютная или относительная погрешность

Сначала нужно определить, какая будет ошибка: строго положительная, отрицательная или в обе стороны. За это отвечает параметр y dir=minus|plus|both.

\addplot +[
	mark=*, 
	only marks,
] plot[
	error bars/.cd,
	y dir=both,
	y fixed=0.1,
%	y fixed relative=0.1,
] table [		    	    	    	
	x=Fr, 
	y=Uin
]{data.tsv};

Здесь указана сразу абсолютная погрешность для всех значений. Аналогично можно задать сразу относительную параметром y fixed relative.

5.3.2. Абсолютная или относительная погрешность из файла

Необходимо явно указать, что ожидается чтение данных ошибки из файла, указать в каком столбце (y error=err) записана ошибка и тип ошибки:

\addplot +[
	mark=*, 
	only marks,
] plot[
	error bars/.cd,
	y dir=both,
	y explicit relative,
] table [		    	    	    	
	x=Fr, 
	y=Uin,
	y error=err,
]{data.tsv};

Для абсолютной ошибки параметр y explicit, для относительной y explicit relative.

5.4. Настройка линии графика

5.4.1. Толщина и цвет линии графика

Толщина линии управляется либо параметром line width=, либо словесными алиасами (рекомендуется использовать именно их):

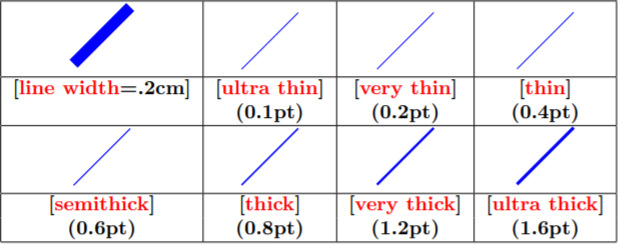
Цвет линии сам является параметром:

\addplot +[
	thick,
	blue!20!black
] plot table [		    	    	    	
	x=Fr, 
	y=Uin,
]{data.tsv};

О составлении цветов сказано ранее в разделе ().

5.4.2. Тип линии графика

Как и цвет, тип линии графика сам по себе параметр:

\addplot +[
	thick,
	blue!20!black,
	dashed
] plot table [		    	    	    	
	x=Fr, 
	y=Uin,
]{data.tsv};

Существует несколько типов линий:

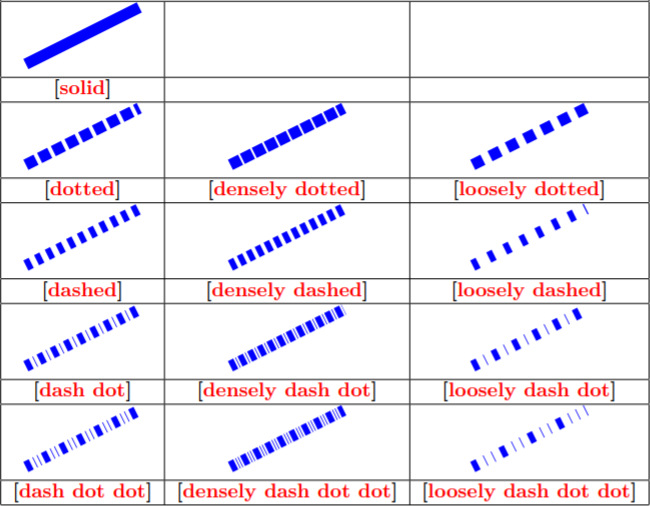
6. Особенности построения графиков

6.1. Построение графиков, терпящих бесконечный скачок

Рассмотрим построение графика с бесконечным скачком на примере построения \(\tan(x)\).

Расчет функций, которые уходят на бесконечность, может привести к ошибкам компиляции. Чтобы этого избежать, можно указать в параметрах принудительное вписывание в пределы расчетов: выйдя за эти пределы, математический движок pgf просто будет пропускать эти значения, пока опять не войдет в пределы:

restrict y to domain=-20:20,

Разумно выбирать эти пределы немного больше заданного предела осей xmin,xmax,ymin,ymax.

Кроме того, можно сказать pgfplots-у, как вести себя при получении бесконечности в расчетах, и не ограничивая расчет:

unbounded coords=discard|jump

Этот ключ настраивает, что делать, если одна или несколько координат одной точки неограничена, или, например, при чтении из файла на этом месте стоит nan или ничего не стоит.

discard (по умолчанию) отбрасывает точку завершения, и в логе компиляции выдается предупреждение. При этом график строится, как если бы неограниченная точка не произошла: pgfplots интерполирует между ограниченными ближайшими точками.

jump просто пропустит значения, которые уходят на бесконечность, и график станет с разрывом.

Однако, как это ни странно, в случае тангенса это все не так: для стандартных функций с разрывом разработчики постарались, и они строятся без дополнительных усилий. Но при этом \(+\infty\) и \(-\infty\) точки графика соединяются, что не всегда может быть полезно: например, обычно в этом месте строят линии асимптот.

Все же придется вернуться к первоначальному определению:

\documentclass[tikz,10pt]{standalone}

\usepackage[T2A]{fontenc}
\usepackage[utf8x]{inputenc}
\usepackage[russian]{babel}

\usepackage{amsmath,amssymb,cmap,pgfplots,pgfplotstable}
\usetikzlibrary{arrows,calc,intersections}
\pgfplotsset{compat=newest}

\begin{document}
\begin{tikzpicture}
\begin{axis}[
	xlabel={$x$},
	ylabel={$\tg x$},  
	axis lines=middle,
	ymax = 10,
	ymin = -10,
	enlargelimits=true,
	xmin=-4*pi/2,
	xmax=4*pi/2,
	restrict y to domain=-20:20,
	xtick=\empty,
	ytick=\empty,
]

\addplot[blue!50,domain={-4*pi/2:4*pi/2},samples=1000] {tan(deg(x))};


\pgfplotsinvokeforeach{-2,-1,...,2}{%
	\draw[dashed, black!20] 
		({{pi/2+pi*#1},0} |- {rel axis cs:0,0}) 
		-- ({{pi/2+pi*#1},0}|-{rel axis cs:0,1});
}

\end{axis}
\end{tikzpicture}	
\end{document}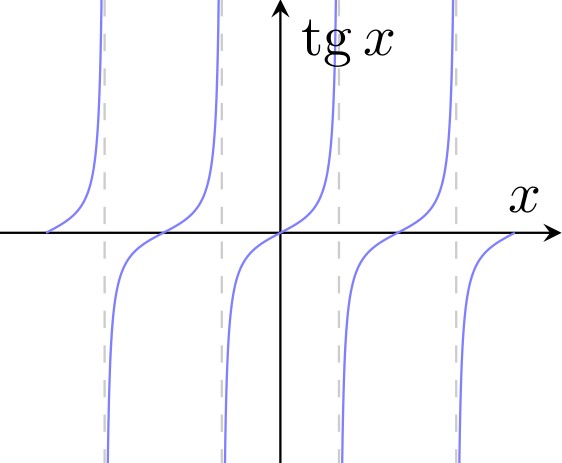

Здесь есть интересный код для построения асимптот. Рассмотрим его подробнее.

6.2. Циклы в pgfplots и построение асимптот. Системы координат рисунка

Стандартный цикл tikz-а, к сожалению, в pgfplots не работает. Приходится использовать его более низкоуровневый аналог:

\pgfplotsinvokeforeach{-2,-1,...,2}{%
	% Выражение в цикле. Счетчик цикла - #1 
}

Счетчик пробегает указанные значения. Можно указывать их как список {0,1,2,3},а можно указать первое значение, второе, троеточие, последнее: из первого и второго рассчитается шаг и счетчик пробежит нужные значения. Они могут быть дробными.

Теперь подробнее, как же работает код построения вертикальной асимптоты. В tikz есть интересный способ расчета координаты в угле. Если задана такая координата X: (A -| B), то она находится в точке, которая образована пересечением горизонтальной линии через A и вертикальной через B:

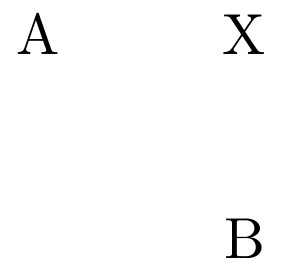
Можно наоборот, (B -| A), соотв. вертикальная через А и горизонтальная через B.

По умолчанию используется система координат осей, в которой начало и орты отвечают нарисованным на графике.

Есть еще так называемая rel axis cs - система координат рисунка: в ней точка (0,0) это левый нижний угол рисунка, а (1,1) - верхний правый.

Со всей этой информацией теперь нетрудно должно быть понять, как работает асимптота через точку x:

({x},0} |- {rel axis cs:0,0}) -- ({x},0}|-{rel axis cs:0,1});

6.3. Использование команд TikZ на графиках Pgfplots

Ровно в предыдущем параграфе рассмотрено применение команд tikz для построения асимптот в осях графика.

Часто возникает еще потребность подписать какие-либо точки на кривой. Для этого можно создать ноду на кривой, где положение ноды задается от 0 до 1 - 0 в начале кривой, 1 в конце. Эдакие криволинейные координаты.

\addplot[blue!50,domain={-4*pi/2:4*pi/2},samples=1000] {sin(deg(x))} 
	node[pos=0.3] (1) {}  
	node[pos=.3,left,black]{$x$};

\draw[fill=magenta] (1) circle (1pt);

Здесь мы специально создали пустую ноду с координатой (1), в которой потом можно нарисовать точку, а вторая нода уже рисует текст.

Для понимания это может быть затруднено, если вы не изучали tikz. Тогда можно просто использовать этот пример, не заботясь принципами его работы.

На кривую так можно поместить сколько угодно точек, главное, в конце списка должна стоять точка с запятой.

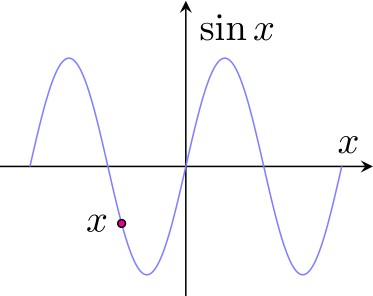
6.3. Качественные графики: удаление меток с осей

Достаточно добавить два параметра к окружению axis:

xtick=\empty,
ytick=\empty,

The End. Рекомендуемые источники

Наконец, прочитав небольшое руководство по использованию pgfplots, вы почти готовы к тому, чтобы применить его для своих работ. В этом нелегком (поначалу) труде смогут помочь некоторые источники.

PGFPlots Gallery. Галерея примеров прямо на сайте: оформление картинка-код, около сотни полезных примеров. ^[return]
Manual for Package PGFPLOTS. Просто-таки необходимое для грамотного использования пакета, полное и подробное руководство, в котором есть все, что только может потребоваться для построения графиков. Информация хорошо структурирована и найти по содержанию информацию о каких-то параметрах и примеры использования совершенно не трудно. ^[return]
The TikZ and PGF Packages Manual. Это весьма полное руководство, в котором можно разобраться с низкоуровневым использованием математики в pgf, а также почерпнуть море информации о использовании tikz. ^[return]
Visual TikZ. Не очень большое, компактное руководство "в картинках". Вместо подробного расписывания на 1000+ страниц, как это сделано в руководстве PGF, здесь сделан упор на практическое применение, и каждый параметр обязательно сопровождается картинкой-результатом. ^[return]